真直な部材で、ピン接合され、軸力のみを受ける、骨組み構造をトラスと言います。
従って、トラス構造では、曲げモーメントは発生しないとします。
なお、軸力の符号は、一般に、引張りを正、圧縮を負とします。 ■静定トラス (改訂2014-2-30)
(1) 外力を部材方向にベクトル分解し、各部材に作用する引張り力を算出します。
三角形の公式 a/sinθa = b/sinθb = c/sinθc を用いて、
Ta = -F・La/Lc = -F・sinθa/sinθc
Tb = F・sinθa/sinθc = F・sinθa/sinθc
なお、Taの値は、圧縮力の意味で負(-)とした。
応力は、部材の断面積で割って σa = Ta / Aa σb = Tb / Ab
(2) 各部材変位は、フックの法則にて ヤング率Eとして、
δa= Laσa/Ea δb= Lbσb/Eb
(3) 荷重作用点での水平および鉛直方向の変位は、近似的に、→詳細説明
右方向:δh= {δacosθa + δbcosθb} / sinθc
下方向:δv= {-δasinθa + δbsinθb} / sinθc
但し、上式は 変位δaを、負(-)の値にしての代入とした。
*圧縮部材の強度計算: 座屈荷重を Pkとして、 Pk>Tb
オイラーの公式を用いて、 Pk = nπEI/Lb2 但し、両端共ピン接合の故 n = 1
なお、本例(図1)で角度が直角の場合を材力演習問題に見掛けられる。 ■不静定トラス
一例として、図2について説明します。部材に左より添え字A,B,Cを付記して、
力の釣合いは、
水平方向 TA・sinθ- TC・sinθ= 0
鉛直方向 TB + TA・cosθ + TC・cosθ- P = 0
従って、 TB+ 2TA・cosθ - P = 0 -- (1)
変位は、
微小にて近似的に δA= δC= δBcosθ
縦弾性係数の式にて、δA= TALA / AAEA δB= TBLB / ABEB -- (2)
LB = LAcosθ であり、従って、 TB = ABEBTA / { AAEAcos2θ } --- (3)
従って、TA,TBは、連立方程式(1),(3)にて
変位はこれを式(2)に代入で求まります。 ■仮想仕事の原理による解法
単位荷重法で、特定箇所の特定方向の変位δを求める方法手順は下記の通り。
・与えられた外力下に於ける、各部材力Tk、軸方向変位δkを前述の如く算出する。
・求むべき変位の箇所に、その方向の、大きさを1とする外力 F' を想定し、
この仮想外力のみが作用する場合の各軸力T'kを算出する。
・仮想仕事の原理にて、求むべき変位を下記式で算出できる。
δ=k∑ Tk・Tk'・Lk Ek・Ak または δ= k∑δkT'k
なお、 添え字k:部材No. L:部材長さ, A:部材の断面積, E:ヤング率 静定トラスの例の図1の場合、
δa= δaT'a + δbT'b なお、 T'a= sinθa/sinθc T'b= sinθb/sinθc
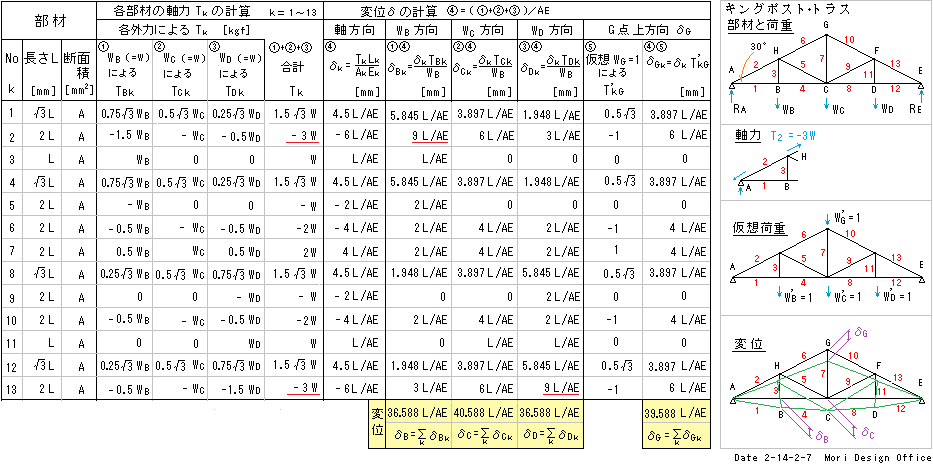
下記は キングポスト・トラスの例で、表中の赤下線で示すように、上弦 AG, GE に大きな力(圧縮)が作用する。 →軸力の算出詳細