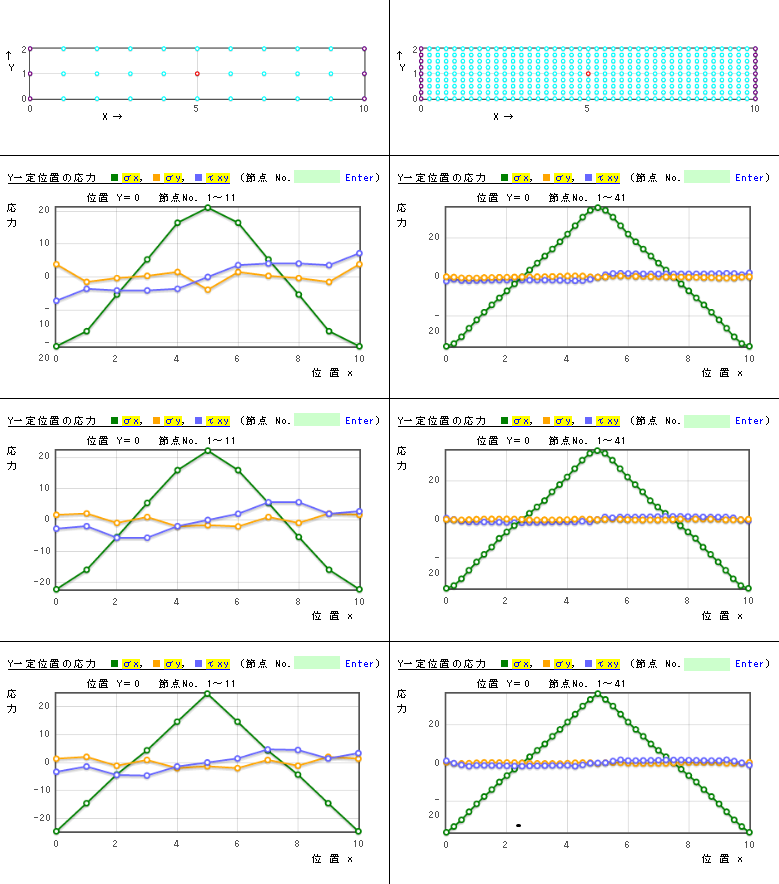
4点求積
4点求積
9点求積
| 両端固定はり (要素数20) | 両端固定はり (要素数320) | |
 | ||
4点求積 | ||
4点求積 | ||
9点求積 | ||
| 要素数20:最大σx、 誤差、 計算時間 | 要素数320:最大σx、 誤差、 計算時間 | |
| ±22.1ton/m2 誤差41% 0.5秒(0.05秒)*1 (±22.0ton/m2)*2 | ±35.3ton/m2 誤差5.9% 7.8秒(2.9秒)*1 | |
| ±24.7ton/m2 誤差34% 0.7秒(0.06秒)*1 | ±36.5ton/m2 誤差2.7% 15秒(1.8秒)*1 |