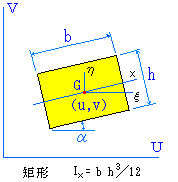
| 断面形状
| 断面2次モーメント I ( 基軸U-V, 添え字g:重心、c:中心または先端 )
|
|
Ixg = ∫-h/2h/2b・y2 dy = b・h3/12
Iyg = h・b3/12
Ixyg = ∫A x・ydA = ∫-b/2b/2
{ x∫-b/2b/2y dy} dx = 0
Iξ = Ixg・cos2α + Iyg・sin2α
Iη =Ixg + Iyg - Iξ
Iξη = (Ixg - Iyg)・sin(-2α)/2
A = b・h
従って、基軸UVに関する断面2次モーメントは、上記値を用いて、Gx=0,Gy=0 故
Iu = Iξ + v2・A Iv = Iξ + u2・A Iuv = Iξη + A・u・v
|
|
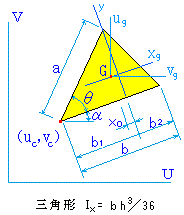
Ixg = ∫-h/32h/3y2・b・(
23-
yh) dy = b・h3/36
尚、h = a・sinθ b1 = a・cosθ yo = h/3 A = h・y/2
Iy = ∫-b10{ x2・(b1-x)・h/b1 } dy
+ ∫0b2{ x2・(b2-x)・h/b2 } dy
= h・b13/12 + h = h・(b13 + b23)/12
Iyg = Iy - xo2・A
= {h・(b13 + b23)/12} - {(-b1+ b2)/3}2・{bh/2}
= h・(b13 + b23 + 2b1 b2b)/36
Ixy1 =∫0h
∫x0
x・y dxdy =
∫0h
[ x 2
2]
-b1(h-y)/h
0dy= -
12
∫0h
{b1(h-y)/h}2
y dy =-b12h2/24
同様に、Ixy2 = b22h2/24
Ixyg = Ixy1 + Ixy1 - xo・yo・A
= -b12h2
24__
+
b22h2
24__
-
-b1 + b2
3____
h
3
bh
2_
= (b12-b22)h2/72
尚、
Gx = ∫0h
bh(h-y)
・y dy = b・h2/6 yo = Gx/A = h/3
Gy = x1oA1 + x2oA2 =
-b13
b1h2
+
b23
b2h2
= hb・(-b1+b2)/6
xo = Gy/A = 2Gy/bh = (-b1+b2)/3
Iug = Ixg・cos2 α + Ivg・sin2 α - Ixyg・sin(-2α) Ivg = Ixg + Iyg - Iug
Iuvg = -12
(Ixg - Iyg)・sin 2α + Ixyg・cos 2α
さて、ug = xg・cos α - yg・sin α vg = yg・cos α + xg・sin α
従って、基軸UVに関する断面2次モーメントは、上記値を用いて、
Iu = Iug + (uc+ug)2・A Iv = Ivg + (vc+vg)2・A
Iuv = Iuvg + (uc+ug)・(vc+vg)・A
|
|
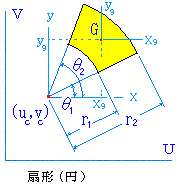
Ixc =
∫θ1θ
2
∫r1r2
r3sin2θ drdθ
= 116(r24 - r14)
[2θ2- 2θ1- sin2θ2+ sin2θ1]
Iyc =
∫θ1θ
2
∫r1r2
= 116(r24 - r14)
[2θ2- 2θ1+ sin2θ2- sin2θ1]
Ixyc =
∫θ1θ
2
∫r1r2
r3cosθ・sinθ drdθ
= -116(r24 - r14)
[cos2θ2- cos2θ1]
Gyc =
∫θ1θ
2
∫r1r2
r2cosθ drdθ
= (r23 - r13)(sinθ2-sinθ1)/3
Gxc =
∫θ1θ
2
∫r1r2
r2sinθ drdθ
= (r23 - r13)(cosθ1-cosθ2)/3
A = (r22 - r12)・(θ2 - θ1)/2
xg = Gyc / A yg = Gxc / A
Ixg = Ixc - yg2・A Iyg = Iyc - xg2・A
Ixyg = Ixyc - xg・yg・A
従って、基軸UVに関する断面2次モーメントは、上記値を用いて、
Iu = Ixg + (vc+yg)2・A Iv = Iyg + (uc+xg)2・A
Iuv = Ixyg + (uc+xg)・(vc+yg)・A
|
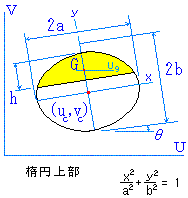
なお、全面 (h=2b ) の場合
面積 A= π・a・b
断面2次モーメント Ix= πab3/4
→式誘導説明
|
A =
2ab
∫b-hb
(b2-y2)1/2dy =
2ab
∫βπ/2
{ (b2-y2)1/2 (dy/dt)dt }y=b・sin t
= a・b2{π - 2β - sin 2β }
Gx =
2ab
∫b-hb
y・(b2-y2)1/2dy =
2ab
∫β
π/2
(b・sin t )・(b・cos t)2 dt =
23a・b2・cos3β
Gy = 0
Ix =
2ab
∫b-hb
y2(b2-y2)1/2 dy=
2ab
∫βπ/2
(b・sin t)2・b・(cos t)
dydt・dt
= 116 a・b3・{ 2π - 4β + sin 4β }
Iy = 2・∫oXex2・{
ab
(a2-x2)1/2 - b + h } dx =
a3・b・(α -
sin 4α4)/4
- 23
(b - h)・xe3
Ixy = 0
但し、 β= sin-1
( b-hb)
xe = ab
(b2-y2)1/2
= ab
(2b・h - h2)1/2
α = sin-1(xe/a)
重心位置での断面2次モーメントは、
Ixg = Ix - yg2・A Iyg = Iy - xg2・A
Ixyg = Ixy - xg・yg・A
なお、 xg = 0 yg = Gx / A
uc,vc からの重心位置は、
ug = xg cos(-θ) + yg sin(-θ) = -yg sin θ
vg = yg cos(-θ) - xg sin(-θ) = yg cos θ rev.2024-02-16
Iug = Ixg・cos2 θ + Iyg・sin2 θ - Ixyg・sin(-2θ) Ivg = Ixg + Iyg - Iug
Iuvg = -12
(Ixg - Iyg)・sin 2θ + Ixyg・cos 2θ
従って、基軸UVに関する断面2次モーメントは、上記値を用いて、
Iu = Iug + (vc+yg)2・A Iv = Ivg + (uc+xg)2・A
Iuv = Iuvg + (uc+xg)・(vc+yg)・A rev.2024-02-16
|