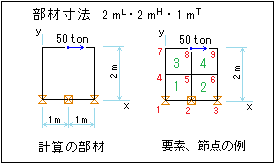
四角形4節点要素、補足説明
節点・応力値の配置
(その2:追加処理)
2011-2-13 Mori Design Office
2次元・有限要素法による応力解析にて ガウス積分点を4点とする応力値が算出されているとし、この応力値を4個の節点数に割当てる。
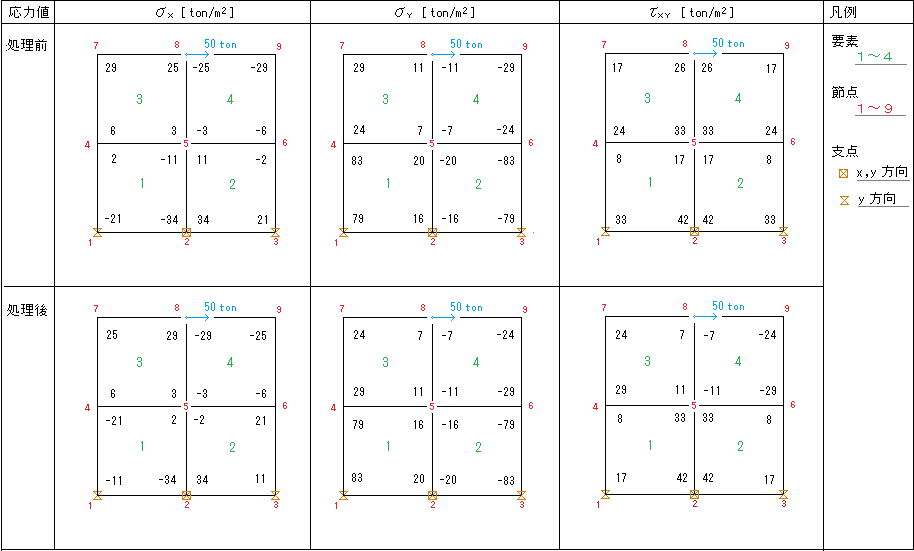
基本処理としては、荷重作用点以外では、連続で平滑な応力分布になるよう応力値を並び替え・配設するとする。さらに追加の処理が必要
であり、荷重作用点での応力値の配置を修正する手順、及びせん断応力値の割当て配置の手順を下記に述べる。プログラムの紹介をする。
|
[基本処理]
①~⑨ n=要素No, j=要素節点No, s=節点No, k=積分点Noとして、s = NodNo[(n-1)*4 + j]、応力σx値 = σx[(n-1)*4+k]、
応力σxについて、要素nの値 = σx_av[n] を用いて、隣接要素B,C の応力に対し平滑連続な分布となるよう、要素Aの応力σx値を
配設する。同様に応力σy,τxyを配設する。 参照→「節点・応力値の配置(大小順位)」
[追加処理]
⑪外部荷重により、節点に作用する内力 fx,fy が求められているとする。例えば、s=節点No として、fx値 = fx[s]
⑫内力の作用する節点は 要素内で応力値が最大または最小となるよう配置修正する。例えば、
要素の右端節点に正値のfx(右方向)が作用の場合は、その節点に引張応力が作用しσxが正値であり、最大値が作用する。
要素の左端節点に正値のfx(右方向)が作用の場合は、その節点に圧縮応力が作用しσxが負値であり、最小値が作用する。
なお、その節点は、両要素で引張と圧縮との2つの値が存在し、応力分布は不連続となっている。
⑬せん断応力τの算出は、応力σx,σyの配設の算出後、σx,σyよりτ大小関係を算出し配設する。
即ち、x方向及y方向で、σx,σy,τの合計が零となる条件で、隣接要素B側方向にτが増加か減少かを算出。
同様に隣接要素C側方向のを算出。これより要素内の節点に対する、τの大小関係の配置が定まり、τ値を割当てる。
|
<html><head>
<title>節点応力-HP</title>
<SCRIPT Language='JavaScript'>
<!---
//----条件データ例-----
//配列値の説明:節点番号=i、n=要素番号、k=四角形要素内の節点番号=kとすれば
//節点i=NodNo[(n-1)*4+k]、応力=σx_org[(n-1)*4+k]、x方向内力=fx[i]、x位置 = x[i]
//本例での単位:位置[m]、内力[ton]、応力[ton/m2]、但し部材厚を1m とする
//①節点番号 (Array最初の0はダミー、要素No1の節点Noは1,2,5,4)
NodNo = new Array(0,1,2,5,4,2,3,6,5,4,5,8,7,5,6,9,8);
NELT = 4;//要素の総数
x = [0,0,1,2,0,1,2,0,1,2]; y = [0,0,0,0,1,1,1,2,2,2]; //節点位置
//②処理前の節点応力値
σx_org = new Array(0,-21,-34,-11,2,34,21,-2,11,6,3,25,29,-3,-6,-29,-25);
σy_org = new Array(0,79,16,20,83,-16,-79,-83,-20,24,7,11,29,-7,-24,-29,-11);
τxy_org = new Array(0,33,42,17,8,42,33,8,17,24,33,26,17,33,24,17,26);
//並び換え処理の応力
σx = new Array();
σy = new Array();
τxy = new Array();
for(k=1;k<=(NELT*4);k++){σx[k] = σx_org[k]; σy[k] = σy_org[k]; τxy[k] = τxy_org[k]; }
//⑪節点に作用する内力 (条件データの追加分)
fx = new Array(0,0,-50,0,0,0,0,0,50,0);
fy = new Array(0,-50,0,50,0,0,0,0,0,0);
var thr= 2;//thresholdを通販プログラムでは1e-6 としている。
//----以下、計算処理 ----------------------
function Node_Stress(){
//③要素についての応力(積分点4か所の応力の平均)
σx_av = new Array();
σy_av = new Array();
τxy_av = new Array();
for( ne=1;ne<=NELT;ne++){
sigx = 0; sigy = 0; tauxy = 0;
for( kk=1;kk<=4;kk++){
sigx += σx[(ne-1)*4+kk]/4;
sigy += σy[(ne-1)*4+kk]/4;
tauxy += τxy[(ne-1)*4+kk]/4;
}
σx_av[ne] = sigx;
σy_av[ne] = sigy;
τxy_av[ne] = tauxy;
}
|
|
kaN = new Array();//節点重なり数
for(i=1;i<=NODT;i++){ kaN[i] = 0;}
for( ne=1;ne<=NELT;ne++){for( k=1;k<=4;k++){kaN[NodNo[(ne-1)*4+k]] += 1;}}
//④隣接する要素の抽出-------内の基本④部分と差替え-------
for( ne=1;ne<=NELT;ne++){
n1 = 0; n2 = 0; aN = 1;
j11 = 0; j12 = 0; j21 = 0; j22 = 0; j31 = 0; j32 = 0; j41 = 0; j42 = 0;
s11 = 0; s12 = 0; s21 = 0; s22 = 0; s31 = 0; s32 = 0; s41 = 0; s42 = 0;
ne1 = ne;
for(nee=1;nee<=NELT;nee++){
nee1 = nee;nee2 = nee;
if(nee1!=ne1){
for(j=1;j<=4;j++){
j1 = j;
j2 = j+1;
if(j1==4){j2 = 1;}
s1 = NodNo[(ne-1)*4+j];
s2 = NodNo[(ne-1)*4+j2];
for(i=1;i<=4;i++){
i1 = i;
i2 = i+1;
if(i1==4){i2 = 1;}
s3 = NodNo[(nee-1)*4+i];
s4 = NodNo[(nee-1)*4+i2];
if((s1==s3 && s2==s4)||(s1==s4 && s2==s3)){
cc = aN;
if(cc==1){
aN = 2; j11 = j1; j12 = j2;//A,B
n1 = nee;s11 = s1; s12 = s2;//B
}
if(cc==2&& (j12==j1||j11==j2)){
aN = 3;j21 = j1; j22 = j2; //A,B,C
n2 = nee; s21 = s1; s22 = s2;//C
}
else if(cc==3&& (j12==j1||j11==j2)){
j31 = j1; j32 = j2; //D
n3 = nee; s31 = s1; s32 = s2;
}
else if(cc>=2){
j41 = j1; j42 = j2; //E
n4 = nee; s41 = s1; s42 = s2;
}
}
}
}
}
}
if(aN>=2){ //④Aに対する隣接要素B,C,D,E、(なお、D,Eは省略可)
//⑥応力σxについて
ne1 = ne;
aA = σx_av[ne]; aB = σx_av[n1]; aC = σx_av[n2];
aD = σx_av[n3]; aE = σx_av[n4];
aAB = aB- aA; aAC = aC -aA;
for(i=1;i<=4;i++){g1[(i-1)] = σx[(ne-1)*4+i]; }
MaxA(); //⑦
j23 = j22 +1; if(j22>3){j23 = j22 +1-4;}
j13 = j12 +1; if(j12>3){j13 = j12 +1-4;}
j14 = j12 +2; if(j12>2){j14 = j12 +2-4;}
if(n3>0&&((j11==j22&&j21==j32)||(j12==j21&&j22==j31))){aAB = (aB-aD)/2; }
if(n4>0&&((j11==j22&&j21==j42)||(j12==j21&&j22==j41))){aAB = (aB-aE)/2; }
if(n3>0&&((j11==j22&&j12==j31)||(j12==j21&&j11==j32))){aAC = (aC-aD)/2; }
if(n4>0&&((j11==j22&&j12==j41)||(j12==j21&&j11==j42))){aAC = (aC-aE)/2; }
//⑧ 図表らん(2)
aCC = 0;if(Math.abs(aAB) < Math.abs(aAC)-1e-10){aCC = 1;}
//⑧ 図表らん(1)上
if( (j12==j21 && 0>=aAC) || (j11==j22 && 0<=aAC) ){
if(aAB>=0){aa = 1; k1 = 0; k2 = 1; k3 = 3; k4 = 2; if(aCC==1){k2 = 2; k4 = 1;}}
if(aAB<0) {aa = 2; k1 = 2; k2 = 3; k3 = 1; k4 = 0; if(aCC==1){k1 = 1; k3 = 2;}}
}
//⑧ 図表らん(1)下
if( (j12==j21 && 0<aAC) || (j11==j22 && 0>aAC) ){
if(aAB>0){k1 = 1; k2 = 0; k3 = 2; k4 = 3; if(aCC==1){ k1 = 2; k3 = 1;}}
if(aAB<0){k1 = 3; k2 = 2; k3 = 0; k4 = 1; if(aCC==1){ k2 = 1; k4 = 2;}}
}
//⑨大小関係・図表の順位に並び換え
σx[(ne-1)*4+j11] = g2[k1];
σx[(ne-1)*4+j12] = g2[k2];
σx[(ne-1)*4+j13] = g2[k3];
σx[(ne-1)*4+j14] = g2[k4];
//⑫荷重点の有無と方向とσx並び換え
if(Math.abs(x[s11]-x[s12])<Math.abs(y[s11]-y[s12]) ){
j3 = j12 + 1; j4 = j12 + 2;
if(j12==3){j4 = 1;}
if(j12==4){j3 = 1;j4 = 2;}
s3 = NodNo[(ne-1)*4+j3]; s4 = NodNo[(ne-1)*4+j4];
if( Math.abs(fx[s4]) < Math.abs(fx[s11]) ){bb = 0;cc = σx[(ne-1)*4+j4];jm1 = j11; dd = σx[(ne-1)*4+jm1];
if ( fx[s11]> 1e-6){bb = 1; if(x[s11]<x[s4]){bb = -1;}}
if ( fx[s11]<-1e-6){bb = 1; if(x[s11]>x[s4]){bb = -1;}}
if((bb== 1 && cc>dd)||(bb==-1 && cc<dd )){ σx[(ne-1)*4+j4] = dd; σx[(ne-1)*4+jm1] = cc;}
}
if( Math.abs(fx[s3])< Math.abs(fx[s12]) ){bb = 0; cc = σx[(ne-1)*4+j3];jm1 = j12; dd = σx[(ne-1)*4+jm1];
if ( fx[s12]> 1e-6){bb = 1; if(x[s12]<x[s3]){bb = -1;}}
if ( fx[s12]<-1e-6){bb = 1; if(x[s12]>x[s3]){bb = -1;}}
if((bb== 1 && cc>dd)||(bb==-1 && cc<dd )){ σx[(ne-1)*4+j3] = dd; σx[(ne-1)*4+jm1] = cc;}
}
}
//荷重点の他の方向(x[s12]-x[s11]),(x[s31]-x[s32]),(x[s41]-x[s42])
//同様にσx並び換え、記述省略
//⑫せん断応力τの配設------------------------------------------------------------------
for(i=1;i<=4;i++){ g1[(i-1)] = τxy[(ne-1)*4+i]; }
MaxA();
j23 = j22 +1; if(j22>3){j23 = j22 +1-4;}
j24 = j22 +2; if(j22>2){j24 = j22 +2-4;}
j13 = j12 +1; if(j12>3){j13 = j12 +1-4;}
j14 = j12 +2; if(j12>2){j14 = j12 +2-4;}
s13 = NodNo[(ne-1)*4+j13]; s14 = NodNo[(ne-1)*4+j14];
s23 = NodNo[(ne-1)*4+j23]; s24 = NodNo[(ne-1)*4+j24];
bb = 1; d1 = Math.abs(x[s12]-x[s11])-Math.abs(y[s12]-y[s11]);
if(d1<0){//AB左右
b2 = (fy[s11]/kaN[s11] + fy[s12]/kaN[s12] + fy[s13] /kaN[s13] +fy[s14]/kaN[s14]);
if(y[s12]-y[s11]<0){b2 = -b2;}
b1 = (σy[(ne-1)*4+j11] - σy[(ne-1)*4+j12] - (σy[(ne-1)*4+j13] - σy[(ne-1)*4+j14]));
if(b1<-thr){bb = -1;}
if(b1> thr){bb = 1;}
if(Math.abs(b1)0){bb = 1;}
else{bb = -1;}
}
}
if(d1>=0){//AB上下
b2 = (fx[s11]/kaN[s11] + fx[s12]/kaN[s12] + fx[s13] /kaN[s13] +fx[s14]/kaN[s14]);
b1 = (σx[(ne-1)*4+j12] - σx[(ne-1)*4+j11] - (σx[(ne-1)*4+j14] - σx[(ne-1)*4+j13]));
if(x[s11]-x[s12]<0){b2 = -b2;}
if(b1<-thr){bb = -1;}
if(b1> thr){bb = 1;}
if(Math.abs(b1)0){bb = 1;}
else{bb = -1;}
}
}
aCC = 0;c2 = null; a2 = σy[(ne-1)*4+j21] - σy[(ne-1)*4+j22];a1 = σx[(ne-1)*4+j21] -σx[(ne-1)*4+j22];
cc = 1;k1 = x[s22]-x[s21]; k2 = y[s22]-y[s21]; d1 = Math.abs(k1)-Math.abs(k2);
if(d1<0){//③
c2 = (fy[s21]/kaN[s21] + fy[s22]/kaN[s22] + fy[s23] /kaN[s23] +fy[s24]/kaN[s24]);
c1 = (σy[(ne-1)*4+j21] - σy[(ne-1)*4+j22] - (σy[(ne-1)*4+j23] - σy[(ne-1)*4+j24]));
if(y[s22]-y[s21]<0){c2 = -c2;}
if(c1<-thr){cc = -1;}
if(c1> thr){cc = 1;}
if(Math.abs(c1)0){cc = 1;}
else{cc = -1;}
}
}
if(d1>=0){//④
c2 = (fx[s21]/kaN[s21] + fx[s22]/kaN[s22] + fx[s23] /kaN[s23] +fx[s24]/kaN[s24]);
if(x[s21]-x[s22]<0){c2 = -c2;}
c1 = ( σx[(ne-1)*4+j22] -σx[(ne-1)*4+j21] ) - (σx[(ne-1)*4+j24] - σx[(ne-1)*4+j23]);
if(c1<-thr){cc = -1;}
if(c1> thr){cc = 1;}
if(Math.abs(c1)0){cc = 1;}
else{cc = -1;}
}
}
d1 = Math.abs(c1)-Math.abs(b1);
if(d1>1e-6){aCC = 1;}
if( (j12==j21 && cc==-1) || (j11==j22 && cc==1) ){
if(bb==1 ){ k1 = 0; k2 = 1; k3 = 3; k4 = 2; if(aCC==1){k2 = 2; k4 = 1;}}
if(bb==-1){ k1 = 2; k2 = 3; k3 = 1; k4 = 0; if(aCC==1){k1 = 1; k3 = 2;}}
}
if( (j12==j21 && cc==1) || (j11==j22 && cc==-1) ){
if(bb==1 ){ k1 = 1; k2 = 0; k3 = 2; k4 = 3; if(aCC==1){ k1 = 2; k3 = 1;}}
if(bb==-1){ k1 = 3; k2 = 2; k3 = 0; k4 = 1; if(aCC==1){ k2 = 1; k4 = 2;}}
}
τxy[(ne-1)*4+j11] = g2[k1];
τxy[(ne-1)*4+j12] = g2[k2];
τxy[(ne-1)*4+j13] = g2[k3];
τxy[(ne-1)*4+j14] = g2[k4];
}
//for( ne=1;ne<=NELT;ne++)の終わり
}
//結果出力のスクリプト(記述省略)-----
//(function Node_Stress()の終)-----------
}
g1 = new Array(3);
g2 = new Array(3);
function MaxA(){
//⑦ 応力値:g1[n]、但しn=0~3。この4個の応力値a,b,c,dを大の順にソート、その順位の応力値=g2[順位]
//プログラム基本構想を参照
}
■計算結果 (上記モデル要素数4の場合の結果。 但し、数値精度には要素数100以上必要。)
|
[要素ごとの節点応力]
|
要素-(k) 節点 |
処理前
σx σy τxy |
処理後
σx σy τxy |
1 - (1) 1
1 - (2) 2
1 - (3) 5
1 - (4) 4 |
-21.0 79.00 33.00
-34.0 16.00 42.00
-11.0 20.00 17.00
2.000 83.00 8.000 |
-11.0 83.00 17.00
-34.0 20.00 42.00
2.000 16.00 33.00
-21.0 79.00 8.000 |
2 - (1) 2
2 - (2) 3
2 - (3) 6
2 - (4) 5 |
34.00 -16.0 42.00
21.00 -79.0 33.00
-2.00 -83.0 8.000
11.00 -20.0 17.00 |
34.00 -20.0 42.00
11.00 -83.0 17.00
21.00 -79.0 8.000
-2.00 -16.0 33.00 |
3 - (1) 4
3 - (2) 5
3 - (3) 8
3 - (4) 7 |
6.000 24.00 24.00
3.000 7.000 33.00
25.00 11.00 26.00
29.00 29.00 17.00
|
6.000 29.00 17.00
3.000 11.00 26.00
29.00 7.000 33.00
25.00 24.00 24.00 |
4 - (1) 5
4 - (2) 6
4 - (3) 9
4 - (4) 8 |
-3.00 -7.00 33.00
-6.00 -24.0 24.00
-29.0 -29.0 17.00
-25.0 -11.0 26.00
|
-3.00 -11.0 26.00
-6.00 -29.0 17.00
-25.0 -24.0 24.00
-29.0 -7.00 33.00 |
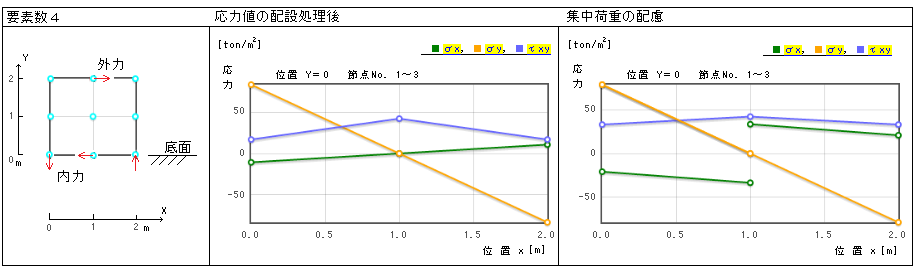
[節点応力]
この結果より節点の応力値がえられる。例えば、底面については下記グラフの如くなる。
なお、中央点のx方向応力は
左グラフでは、σx = (-34+34)/2 = 0 ton/m2
右グラフでは、集中荷重fx が作用しているのを配慮し、左側σx = -34 ton/m2、右側σx = 34 ton/m2
[備考]
・集中荷重について、加圧面積零は応力無限大で理論的に値が存在しない為、微小面上の荷重に置換え想定する。
・ガウス積分が9点での場合は、補間法で応力値4点を算出した後、同様にして節点応力を算出することが出来る。
参照:
FEM要約(四角形)
節点・応力値の配置(大小順位)
節点応力(図表)
求積法の結果比較
FEM計算画面(9点求積法)
Copyright (c) @2007 Mori Design Office, All right reserved


